The International Capital Standard (ICS) introduces a new approach to discounting illiquid liabilities — one that includes an explicit credit risk premium. But how does it compare to Solvency II’s Fundamental Spread? And what might it mean for UK insurers already familiar with the Matching Adjustment? We break down the key differences and their potential impact.
The International Capital Standard (ICS), finalised by the International Association of Insurance Supervisors (IAIS) in December 2024, marks a new chapter for Internationally Active Insurance Groups (IAIGs). While the UK’s five IAIGs may find ICS implementation largely uneventful — given its less demanding capital framework compared to Solvency II (SII) — certain ICS rules offer fresh insights. One area drawing particular interest is how the ICS handles illiquid liabilities and its explicit inclusion of a Credit Risk Premium (CRP) in discount rates.
This article explores:
- How the ICS risk correction for illiquid liabilities works.
- How it compares to Solvency II’s Matching Adjustment (MA) and Fundamental Spread (FS).
- Whether the ICS’s approach offers a more robust or practical alternative.
The ICS risk correction factor for illiquid liabilities
From a UK life perspective, the ICS treatment of illiquid liabilities, and how this compares with the SII (UK) Matching Adjustment (MA), is particularly interesting. Like SII, the ICS allows suitably matched illiquid liabilities to be discounted at a higher discount rate than other liabilities. Again, like SII, this discount rate is based on the yield earned on the assets backing the liabilities and is subject to a risk correction to allow for the credit risk exposures of those assets.
For those familiar with the MA and the Fundamental Spread (FS) reform debates of recent years, the ICS Level 2 text includes an eye-catching paragraph. L2-88 states: “For corporate bonds, the risk correction factor captures the expected loss and the credit risk premium. The expected loss is determined assuming an annualised probability of default for a theoretical 10-year bond and a loss given default of 70%. Credit risk premium is based on one standard deviation of the loss distribution.”
In contrast to the Matching Adjustment, L2-88 requires the explicit inclusion of the asset’s credit risk premium (CRP) in the risk correction element of the illiquid liability discount rate. This was something that the PRA had argued in favour of during the FS reform debates of recent years (See paragraph 18, DP2/22 – Potential Reforms to Risk Margin and Matching Adjustment within Solvency II and Solvency II Review: Matching adjustment and reforms to the fundamental spread). As Sam Woods, the CEO of the PRA, candidly noted recently, the PRA lost the argument for Fundamental Spread reform “hands down”.
Below we discuss how the particular approach to measuring the CRP described in the ICS Level 2 text may be implemented; how the resultant risk correction compares to the Fundamental Spreads of the Solvency II MA; and, finally, whether the ICS could have implemented simpler alternative approaches to determining CRP allowances in the risk correction factors.
Implementing the ICS risk correction factor
The ICS risk correction factor has two components: an expected default loss (EDL) (which is comparable to the probability of default (PD) component of the MA FS) and the CRP. The ICS Level 2 text defines a measure of CRP in a specific statistical way. This CRP definition is related to the level of default risk of the asset but otherwise doesn’t have an obvious theoretical basis.
There is also a potentially important ambiguity within the definition – the standard deviation of the loss distribution referred to in the Level 2 appears to be that relating to a single asset rather than a diversified portfolio. Common sense would suggest the latter is a more natural measure – after all, the CRP exists to reward non-diversifiable default risk, not issuer-specific default risk.
The charts below highlight that the difference between these two measures is highly material. The first chart compares the probability distributions for the realised rate of return on a single zero-coupon A-rated bond and a well-diversified portfolio of A-rated bonds. These probability distributions assume the bonds are bought and held until the maturity date and that the proceeds of a default are equal to the cost of a risk-free bond that pays a cashflow at the original bond maturity date equal to 30% of the defaulted bond’s contractual cashflow. The credit rating transition matrix is calibrated to S&P’s average multi-year global corporate bond transition matrix (1981 – 2023); and a one-factor correlation model has been used to model the joint behaviour of the well-diversified bonds, assuming a correlation of +0.3.
Chart 1: Cumulative probability distribution of the 10-year annualised realised rate of return on 10-year zero-coupon bonds

The credit transition matrix implies a single A-rated bond has a 1.4% probability of defaulting over a 10-year period. If this occurs, the loss of 70% of the contractual cashflow reduces the internal rate of return from 5.4% to -6.6%. The well-diversified portfolio, unsurprisingly, has a very different and less severe downside risk profile. The assumption of a positive correlation in the default experience of the bonds results in some material non-diversifiable risk, but the left-hand tail is nonetheless much less severe than in the case of the single bond.
The second chart plots the same data in a different way: it shows the 10-year annualised default loss distributions produced by a single A-rated bond and a portfolio of well-diversified A-rated bonds. These loss distributions are intended to correspond to the loss distributions referred to in the ICS Level 2 text.
Chart 2: Cumulative probability distribution of the 10-year annualised loss distribution on 10-year bonds

The above chart highlights the obvious point – the loss distribution produced by a single bond is much riskier than that produced by a well-diversified portfolio of bonds. These different loss distributions result in very different quantifications of the ICS measure of the CRP (which refers to the standard deviation of this loss distribution): the portfolio measure produces a CRP estimate of 14bps for 10-year A-rated bond, whereas the single bond measure produces a corresponding result of 139bps.
While the ICS Level 2 text makes no mention of a diversified portfolio when defining this risk measure, we conclude here that the single bond approach produces untenably large risk correction measures. We therefore assume that the ICS implementation intends for diversified portfolios to be used in the determination of the standard deviation of the loss distribution for the purposes of defining the CRP component of the risk correction.
How does the ICS risk correction compare to the Solvency II Fundamental Spread?
We next consider how the ICS risk correction compares with the Solvency II Fundamental Spread (FS). We have used the multi-year credit modelling described above to determine the ICS risk corrections for a range of credit ratings (again, all assumed to be 10-year zero-coupon bonds).
Chart 3 compares the ICS risk correction results alongside the SII FSs as published at 31 December 2024 for non-financial GBP corporate bonds. (These results are also provided in tabular form in an appendix.)
Chart 3: SII Fundamental Spreads and ICS Risk Corrections for 10-year non-financial zero-coupon corporate bonds

The analysis suggests that the ICS risk correction is less onerous than the SII FS for AAA, AA and A credit ratings – despite the explicit inclusion of a CRP element in the risk correction. Diving into this a little further, we can compare the various components that make up each:
- As noted earlier, the ICS EDL is fundamentally similar to the SII PD, and we assume the same values for these elements.
- The remaining part of the ICS risk correction is the allowance for the CRP; and the remaining parts of the SII FS are the Cost of Downgrade (CoD) and the Long-Term Average Spread (LTAS) components. For AAA, AA, and A-rated bonds, the CoD is broadly equivalent to the ICS CRP, and it is the inclusion of the LTAS that generates most of the margin over which the SII FS exceeds the ICS risk correction.
The above analysis is a comparison at a single point in time and it only considers bonds with 10-year terms to maturity. Nonetheless, the tentative conclusion is quite interesting – for 10-year investment grade credit, the implicit margins that are included in the SII FS calibration tend to exceed the explicit allowance for a CRP that is introduced in the ICS risk correction. This result may differ over time and for different terms of bonds. It also raises the question of whether the somewhat esoteric approach to defining the CRP in the ICS risk correction produces sensible economic estimates. We consider this point next.
A simpler approach to implementing a credit risk premium estimate?
The discussion above highlighted that operationalising the ICS risk correction factor, and in particular quantifying its CRP component, is complicated to implement. It also does not have a clear theoretical basis. It behoves us to consider whether another approach could work better.
A simple approach to empirically estimating the CRP in corporate bonds can make use of the economic link between credit-risky assets and equities. Such a link can allow us to piggyback off the equity risk premium – which is arguably a more straightforward and empirically well-researched economic variable. There has been significant academic research on the theoretical link between credit risk and equity risk. The early option pricing theory research of Black, Scholes and Merton was primarily motivated by the recognition that corporate equity and corporate debt had option-like payoffs.
Empirically, the link between the risk premium for bearing credit risk and the equity risk premium can be determined with reference to the beta of credit-risky assets with respect to an equity index. And this empirical relationship between a credit-risky asset’s credit rating and its equity beta has been the subject of considerable academic research.
What about the equity risk premium? Typical academic estimates (see, for example, Triumph of the Optimists, by Dimson, Marsh and Staunton) for the equity risk premium range from 3% to 5% or so. These are unconditional (or through the cycle (TTC)) forward-looking estimates. In the context of making a risk correction to a market spread, we are arguably more interested in a point-in-time (PIT) equity risk premium estimate (and we may also consider how this PIT equity risk premium likely changes in market stresses, so that we can apply a stressed risk factor in credit spread stresses).
The real yield gap – the difference between the equity dividend yield and the long index-linked bond yield – is a simple starting point for developing a PIT measure for the equity risk premium. At the end of the 2024, the FTSE All-Share had a dividend yield of 3.6% and the long index-linked gilt yield was 1.7%. Assuming a real dividend growth assumption in line with a long-term GDP growth of 1.4% implies a current PIT equity risk premium of 3.3%. This is at the low end of typical long-term TTC estimates, but current market valuations (in equity and corporate bond markets) are high by historical standards.
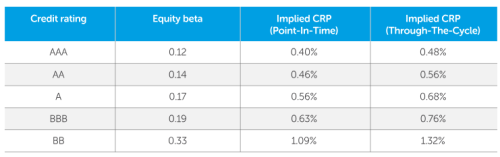
There have been several empirical academic studies of corporate bonds’ equity beta. The table below shows some estimates for the equity betas of credit-risky debt and the CRPs implied by the PIT equity risk premium of 1.9% discussed above and a 4.0% TTC equity risk premium. These use global corporate bond equity beta estimates published in a 2020 European Central Bank Working Paper.
Table 1: Some estimates of equity betas and CRPs by credit rating
The chart below compares and contrasts the CRP estimates produced by these approaches with those produced using the ICS definition. We also compare these with the Solvency II CoD + LTAS components, i.e. the FS in excess of the PD.
Chart 4: Comparison of CRPs and FSs in excess of PDs
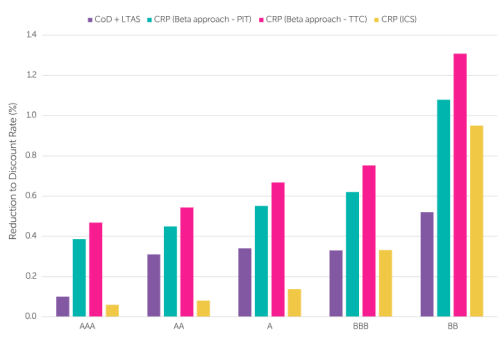
So, four different approaches to estimating CRPs, and four different sets of results!
The extent to which we care about whether robust estimates of CRPs are included in our illiquid liability discount rate risk corrections ultimately boils down to how much we really want to construct a market-based VaR capital estimate – as opposed to dressing a run-off capital calculation in VaR clothing. From a market-consistent valuation perspective, it is interesting to note that the liability valuations produced by the MA are typically lower than transaction prices in the bulk annuity market. Using the CRPs produced by the equity beta approaches (instead of the CoD + LTAS of the FS) will likely result in liability valuations that reconcile more closely with current annuity market pricing. That doesn’t necessarily mean they are a ‘better’ risk correction measure – but it does suggest they more closely align with a market-based liability valuation approach.
Concluding remarks
Our analysis suggests a slightly ironic result: despite explicitly incorporating a loading for CRP in the illiquid liability discount rate risk correction – a feature the PRA advocated for but which wasn’t implemented in the Solvency UK reforms — the ICS risk corrections are less onerous than SII’s FSs for investment grade bonds (at least currently for 10-year duration GBP non-financials).
The approach taken in the ICS to defining a CRP does not have a clear theoretical foundation, and we believe there are arguably more conceptually robust approaches that can be taken that are also more straightforward to implement (and will tend to produce higher CRP estimates for investment grade quality assets). But the policy decision to include an explicit CRP in the risk correction is nonetheless an interesting development that provides a notable benchmark for future prudential policy development.
Craig Turnbull is Partner and Head of Regulatory Advisory at Barnett Waddingham
Amit Lad is Principal, Insurance and Longevity Consulting at Barnett Waddingham
Appendix
Table A.1: Composition of Solvency II Fundamental Spread and ICS Risk Correction by credit quality for a 10-year non-financial zero-coupon bond (bps)

Any views expressed in this article are those of the author(s) and may not necessarily represent those of Life Risk News or its publisher, the European Life Settlement Association

